The Bathtub Curve

In reliability context, the so called bathtub curve is an idealized representation of the failure rate (or MTBF) of a population of items over time.

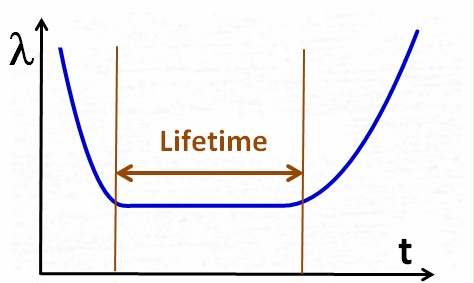
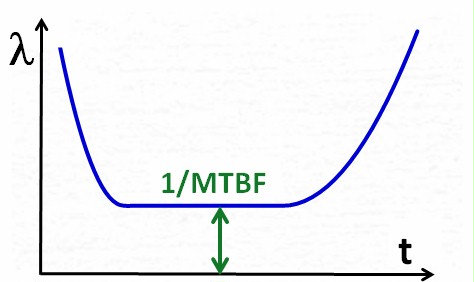
The bathtub curve has three phases, each of them representing a product life phase. Lambda = failure rate = 1/MTBF, and t = time.

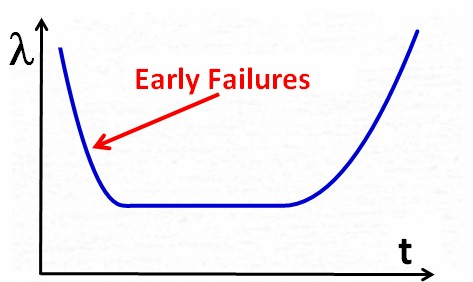
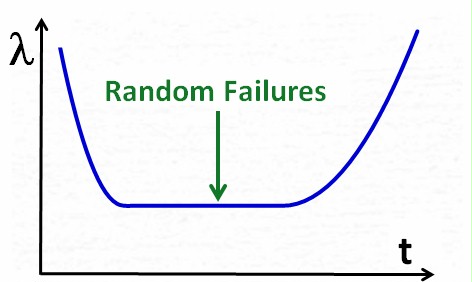
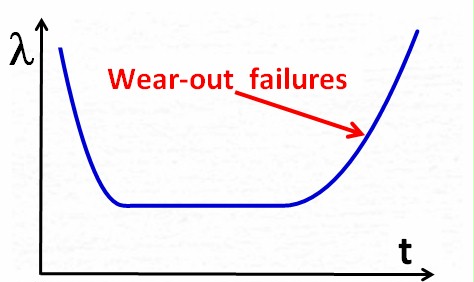
Early failures, also called infant mortality, are typical for immature products with design flaws.	The useful product life phase. This and only this life phase should customers encounter with their product.	Old products beyond their useful lifetime.

As said, this curve is idealized. Most real curves are not that smart.

Apart from the 3 product life phases, the bathtub curve shows an even more important topic: Lifetime and MTBF are *obviously* not the same.

While Lifetime is just the duration of the product life (the t-axis), MTBF (or it's reciprocal lambda, failure rate) is a function of t.

The difference boils down to this:

The MTBF is the mean time between two failures during the useful product life phase.

MTBF depends strongly on the complexity (= # of single components) of the system, whereas Lifetime is always in the same range regardless of the type of product, typically between 10 and 30 years. The table below gives some examples.

The bathtub curve is actually a sum of three individual curves

1. The early failures curve starts at a high value at t = 0 and then  decreases to zero with time --> infinity
2. The wear-out failures curve starts with value 0 at t = 0 and  increases to infinity with t --> infinity.
   
3. The constant failure rate curve is actually a horizontal line for every t, but is dominated by the eary failures curve for small t and by the wear-out failures curve for large t
   

All three individual curves can be expressed by the Weibull distribution, however with different form factors: